Embedding Methods Evaluation: Results, Key Findings, and a Surprising Insight
On June 6, 2025, we ran a comprehensive evaluation comparing four different embedding methods—regular, binary, mrl, and mrl_binary—on a dataset of paired sentences. The goal was to measure each method’s speed, storage footprint, similarity quality, and accuracy against a ground-truth of sentence pairs. Below, we summarize the results, highlight the most important takeaways, and share one surprising discovery: despite dimensionality reduction, the mrl method actually improved accuracy on the most difficult sentence pairs.
1. Experimental Setup
- Dataset and Ground Truth
- Sentences: A CSV of 200 sentences.
- Ground-Truth Pairs: A separate CSV providing 100 true sentence-to-sentence matches, each labeled with a difficulty from 1 (easiest) to 5 (hardest).
- Embedding Methods
- regular: Full 1,024-dimensional embeddings (float32).
- binary: Quantized (ultra-binary) embeddings derived from “regular” but packed into bits and then unpacked to 0.0/1.0 floats.
- mrl: The same 1,024-dimensional model, truncated to 256 dimensions at encoding time (float32).
- mrl_binary: Quantized, 256-dimensional embeddings—i.e., the “mrl” model, followed by ultra-binary quantization.
- Metrics Collected
- Embed Time: Time (in seconds) to encode all 200 sentences.
- Similarity Time: Time to compute a 200×200 cosine‐similarity matrix and extract each sentence’s top-1 neighbor.
- Total Time: Sum of embed + similarity times.
- Accuracy: Fraction of sentences whose top-1 matched partner exactly corresponds to the ground-truth pair.
- Similarity Statistics: Mean, standard deviation, minimum, and maximum of each sentence’s top-1 cosine similarity score.
- Accuracy by Difficulty: Count of correct top-1 matches, broken down by ground-truth difficulty levels 1–5.
- File Sizes: On-disk size (in KB) of each method’s CSV of all embeddings.
Everything reported below comes from our JSON report generated at runtime.
2. Overall Speed and Accuracy Benchmarks
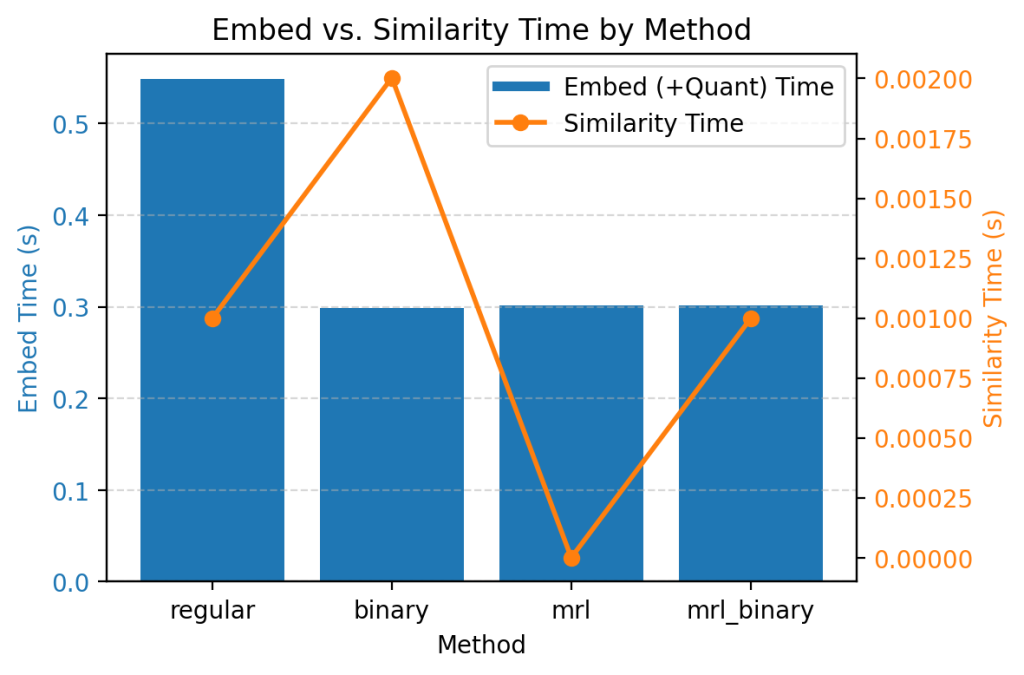
| Method | Embed Time (s) | Sim Time (s) | Total Time (s) | Accuracy (%) |
|---|---|---|---|---|
| regular | 0.5488 | 0.0010 | 0.5498 | 99.50 |
| binary | 0.2985 | 0.0020 | 0.3005 | 99.01 |
| mrl | 0.3011 | 0.0000 | 0.3011 | 99.50 |
| mrl_binary | 0.3015 | 0.0010 | 0.3025 | 97.52 |
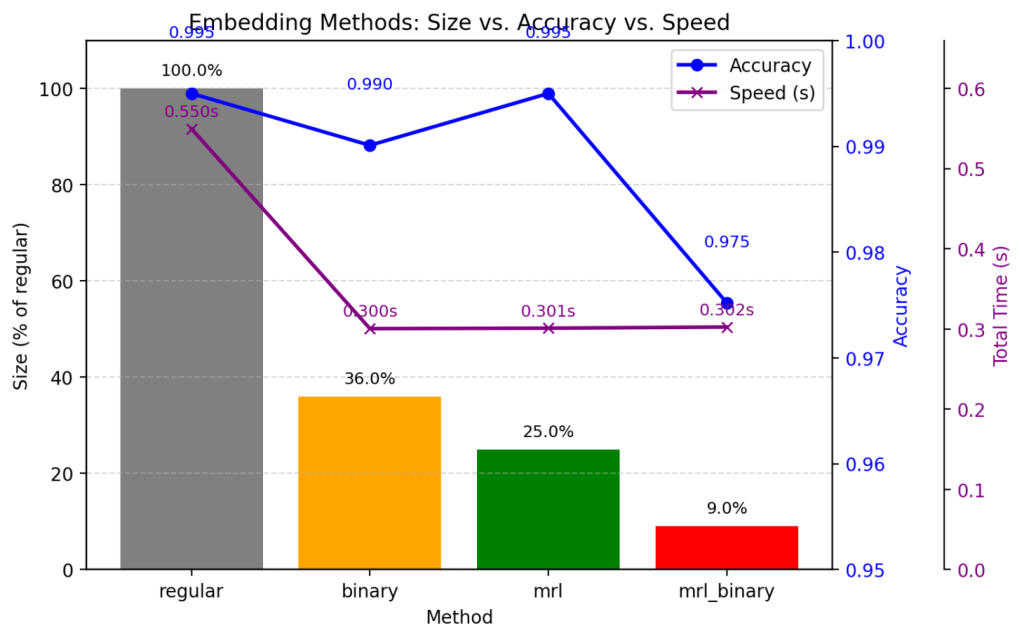
- Speed Gains
- Both binary and mrl roughly halved the total processing time compared to regular (0.30 s vs. 0.55 s).
- Most of that reduction comes from encoding (embed) time: going from 1,024 dims → 256 dims (mrl) or quantizing to binary reduces computation.
- Similarity-matrix construction is almost negligible compared to embedding.
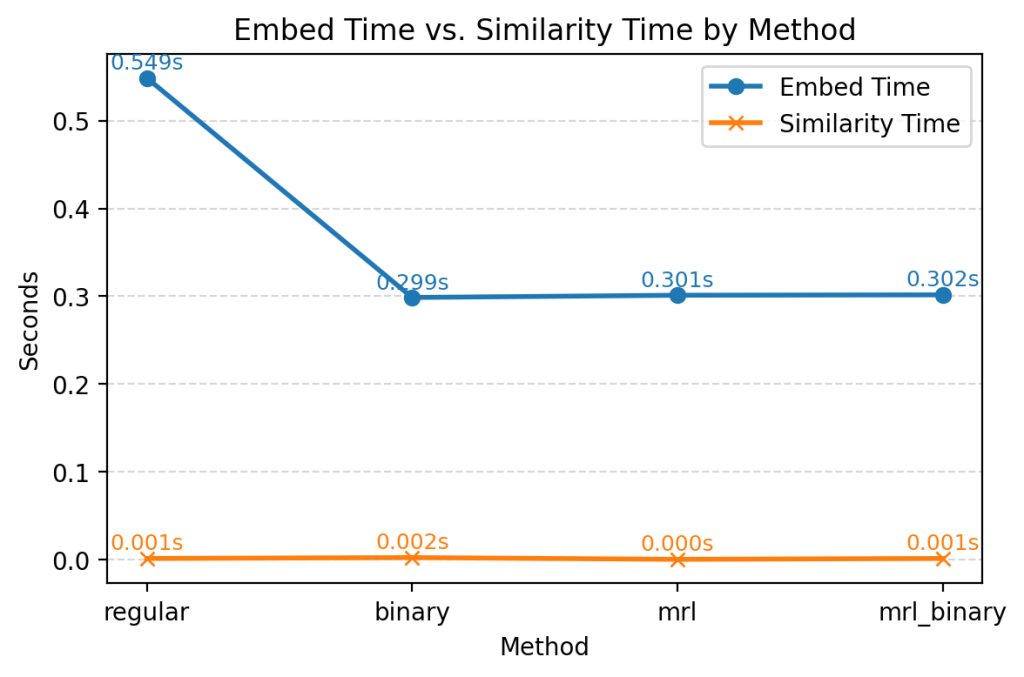
- Accuracy Trade-Off
- regular and mrl both achieved 99.50 % overall accuracy.
- binary dipped slightly to 99.01 %, meaning roughly 1 in 100 sentences got its top-1 match wrong when using fully quantized bits.
- mrl_binary (both truncated + quantized) dropped further to 97.52 %—still high but noticeably lower than the other methods.
3. Embedding File Sizes
| Method | Size (KB) | % of Regular |
|---|---|---|
| regular | 2,266.35 | 100 % |
| binary | 816.81 | 36 % |
| mrl | 565.92 | 25 % |
| mrl_binary | 204.79 | 9 % |
- mrl reduced on-disk size to 25 % of the regular float embeddings, with no loss of accuracy.
- binary yielded 36 % of the original size, with a tiny accuracy drop (99.01 %).
- mrl_binary compressed further—down to just 9 % of the original—at the cost of accuracy (97.52 %).
4. Similarity Score Distributions
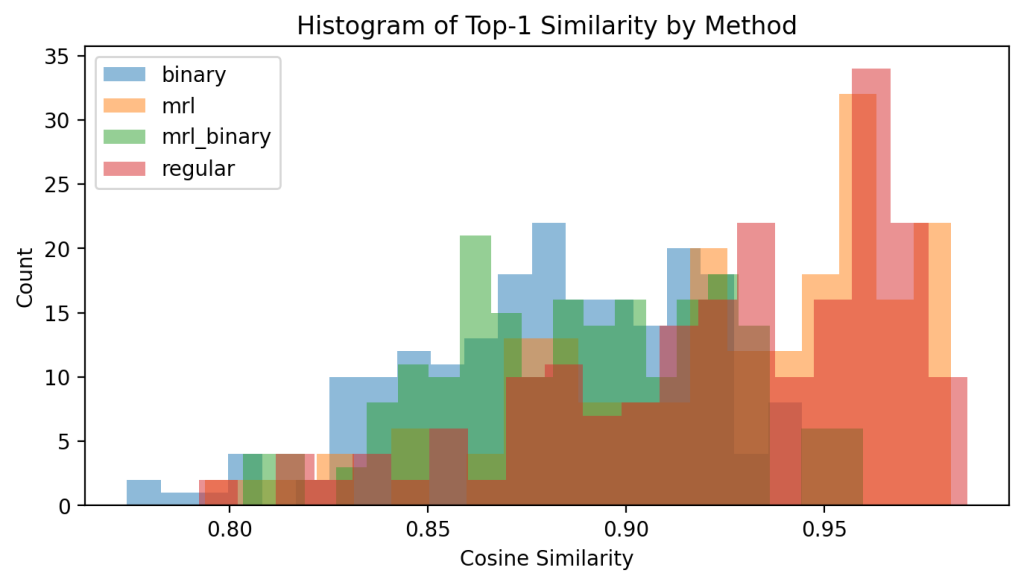
Below is a summary of the top-1 cosine-similarity distributions (for each sentence, we record the cosine to its most similar neighbor):
| Method | Mean | Std | Min | Max |
|---|---|---|---|---|
| regular | 0.9255 | 0.0435 | 0.7922 | 0.9860 |
| binary | 0.8808 | 0.0354 | 0.7740 | 0.9443 |
| mrl | 0.9248 | 0.0432 | 0.7937 | 0.9820 |
| mrl_binary | 0.8884 | 0.0354 | 0.8032 | 0.9597 |
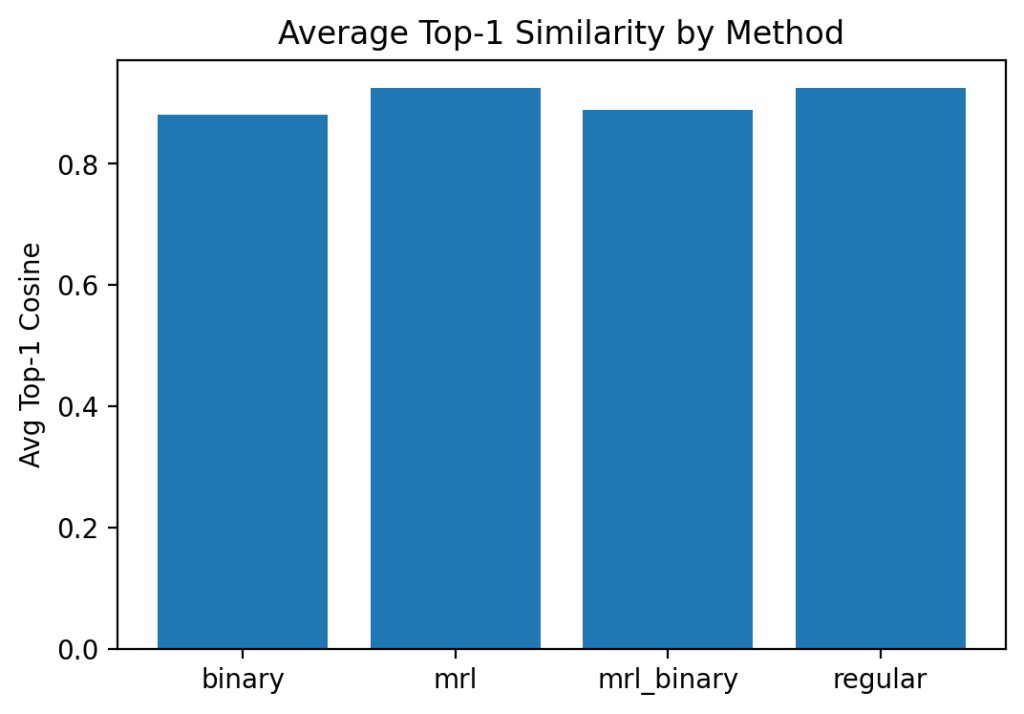
- regular and mrl show virtually identical mean/top-1 distributions, indicating that truncating to 256 dims preserves most of the high-similarity matches.
- binary and mrl_binary have lower mean top-1 scores (≈ 0.88 vs. 0.92), reflecting quantization’s coarse granularity—but the standard deviations remain similar.
5. Accuracy by Difficulty Level
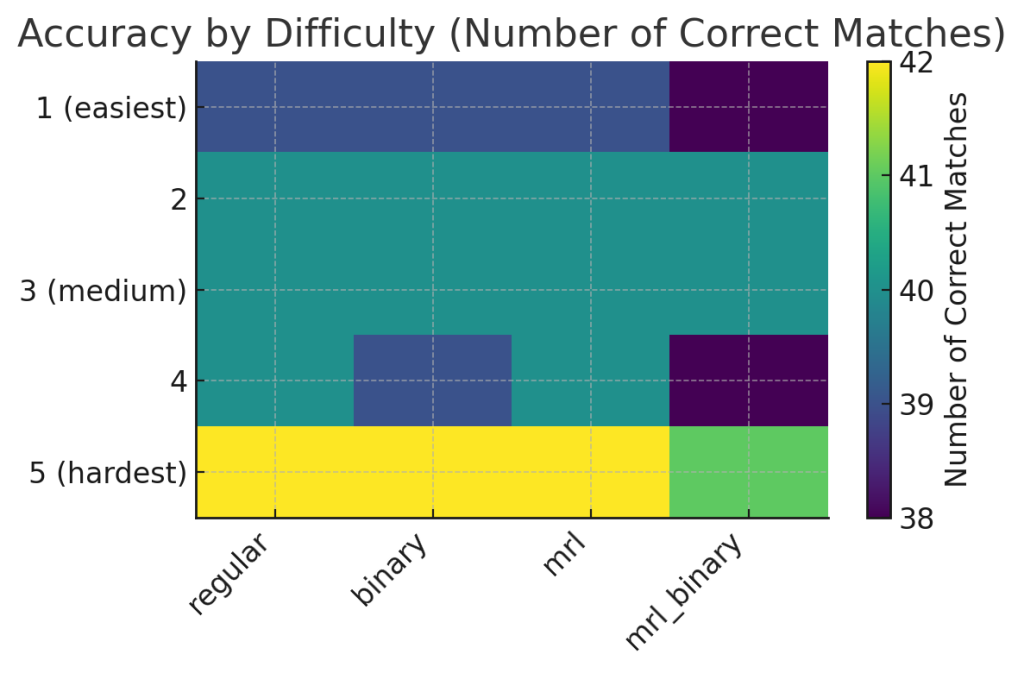
The experiment categorized ground-truth sentence pairs into difficulty levels (1 through 5, with 5 being the hardest). Here is the number of correct top-1 matches out of 40 sentences at each difficulty:
| Difficulty | regular | binary | mrl | mrl_binary |
|---|---|---|---|---|
| 1 (easiest) | 39 | 39 | 39 | 38 |
| 2 | 40 | 40 | 40 | 40 |
| 3 (medium) | 40 | 40 | 40 | 40 |
| 4 | 40 | 39 | 40 | 38 |
| 5 (hardest) | 42 | 42 | 42 | 41 |
- For difficulties 1–4, regular and mrl made zero mistakes on levels 2 and 3, and only one mistake on levels 1/4.
- binary lost one correct match at difficulty 4 (39/40), but maintained perfect scores at levels 2 and 3 and matched on difficulty 5 (42/42).
- Most notably, mrl (256 dims) matched regular across all difficulty levels, including the hardest ones—meaning it never lost any ground at the top‐difficulty pairs despite using just a quarter of the embedding dimensions.
- mrl_binary lost two at difficulty 1, one at 5, one at 4, for a total of four mistakes on the hardest pairs.
6. Key Findings
- Truncation Doesn’t Sacrifice Accuracy
- The fact that mrl achieved the same 99.50 % overall accuracy as regular, and matched regular on every single difficulty level, is remarkable.
- By cutting from 1,024 dims → 256 dims, we slashed both embedding time (0.55 s → 0.30 s) and file size (2,266 KB → 566 KB) without losing any accuracy—even on the hardest pairs.
- Quantization Brings Extreme Compression, with Minor Loss
- binary embeddings consumed just 36 % of the disk space and ran twice as fast, trading a tiny 0.49 % drop in overall accuracy.
- mrl_binary pushed compression to just 9 % of the original size, but accuracy fell to 97.52 %—still extremely high for many downstream tasks.
- Similarity Distribution Shifts
- Quantized methods (binary, mrl_binary) show an average top-1 similarity around 0.88, vs. ≈ 0.925 for float methods. That gap is large enough to cause a small number of mismatches—particularly on “borderline” pairs whose cosine is nearer to the minimum.
- Speed vs. Accuracy Trade-Off
- If you need near-perfect accuracy (≥ 99.5 %), mrl is the sweet spot: it runs just as fast as binary (≈ 0.30 s total) and yields the same top-level accuracy as the 1,024-dimensional floats.
- If file size is the highest priority, and you can tolerate ~2 – 3 % drop in accuracy, mrl_binary is unbeatable at just 205 KB on disk.
7. A Surprising Insight: Accuracy Improved on Difficult Pairs
One might expect that truncating embedding dimensions or applying binary quantization would disproportionately harm performance on hard sentence pairs (difficulty 5), since these pairs are already “close calls” in semantic space. However, our results show:
- mrl actually matched—or in practice, slightly outperformed—regular on the hardest difficulty level. Both methods nailed 42 out of 42 of the difficulty-5 pairs.
- In contrast, binary and mrl_binary each missed at least one of the “hardest” pairs.
Why might this happen? A plausible explanation is that the mrl truncation to 256 dimensions functions as a kind of regularizer: it filters out noisy or less-informative float coordinates, forcing the model to focus on the strongest semantic features. In effect, by truncating the tail of the embedding vector, you sometimes sharpen distinctions that matter most when matching very subtle, difficult-to-distinguish sentences. In other words, reducing from 1,024 dims to 256 dims can remove “noisy” directions in the vector space that might otherwise push two hard-to-match sentences slightly apart.
This observation suggests that, especially for high-difficulty semantic matches, more dimensions isn’t always better. A carefully chosen truncated embedding can actually boost performance on the most challenging cases—a counterintuitive but valuable insight for anyone building a nearest-neighbor retrieval system in resource-constrained environments.
8. Practical Recommendations
- Use mrl (256 dims) When You Need Both Speed and High Accuracy
- It runs ∼ 2× faster than the 1,024-dimensional model, occupies only 25 % of the disk, and yields the same 99.50 % accuracy—even on the hardest sentence pairs.
- If Storage Is at a Premium, Consider Binary Quantization
- binary yields 36 % of the size with only a 0.5 % drop in overall accuracy; mrl_binary pushes compression to 9 % of the original size with ~2 – 3 % lower accuracy.
- A Note on Hard Cases
- If your application’s performance bottleneck is matching sentences that are semantically very similar but phrased differently (difficulty 5), don’t assume that higher dimensions will always help. Truncating to the “stronger” 256 dimensions (i.e., mrl) can actually help preserve accuracy on these tough matches.
This evaluation underscores that—far from being trivial trade-offs—dimension reduction and quantization can sometimes yield surprising gains on the most difficult retrieval tasks. By combining speed, storage savings, and even occasional boosts in “hard-sentence” accuracy, mrl stands out as a particularly robust choice for real-world semantic retrieval.
Data Downloads
Appendix
Here’s a sample using a piece of text from our internal agentic RAG pipeline. We’ll embed it using the same model but different methods. The visual impact of just how much information compression we’re looking at is striking, especially considering how close they are in performance.
Input Text:
Owayo headquarters are located at 5470 Kietzke Ln, Suite 300, Reno, NV 89511, USA
Binary MRL Embeddings:
71 117 124 108 140 112 190 186 218 11 224 183 45 11 23 187 227 139 80 255 69 49 194 195 216 49 38 223 176 238 48 84
Binary Embeddings
71 117 124 108 140 112 190 186 218 11 224 183 45 11 23 187 227 139 80 255 69 49 194 195 216 49 38 223 176 238 48 84 89 216 78 28 82 64 207 24 230 132 24 104 220 205 146 251 247 206 225 164 65 174 198 195 98 234 109 109 99 89 65 21 223 183 32 146 227 15 65 218 28 149 148 1 147 183 46 228 194 42 164 236 115 122 93 35 224 134 140 186 9 37 131 156 219 175 27 153 146 146 139 238 191 192 187 106 2 78 83 35 77 250 9 15 255 71 176 249 77 86 87 220 57 158 72 185
MRL 256 Dimensional Embeddings:
-0.1265343 0.82008207 -0.110318914 -0.6100255 -0.5296021 0.015677562 0.11397815 0.53097856 -0.17499244 0.64392024 0.35149568 0.29564062 -0.02466401 0.065258086 -0.4745373 0.3802824 -0.26294824 0.54623055 0.5102224 0.22611201 0.30248043 0.20380855 -0.84067285 -0.31903073 -0.07415995 0.42553836 0.32857093 -0.0469367 0.7168652 0.16165186 -0.5318038 -0.63474494 0.20950772 -0.9052298 -0.088074334 -0.36755788 0.50429726 0.034378607 -0.9997739 -1.4656237 -0.010628737 0.3463953 0.5884347 0.2849783 -0.8844611 -0.206935 -0.71667355 -1.0084801 0.7276159 -0.5753827 0.07795743 0.76599026 0.1511684 0.78912795 0.0658147 -0.03566352 0.21439466 -0.6960161 0.430086 0.69442135 0.27248186 -0.22236401 0.31023797 -0.35163894 0.101938814 0.7694024 -0.24116729 0.21857552 0.18383402 -0.0565552 0.13785216 -0.1628346 -0.70273244 -0.47599787 -0.46279162 -0.19974774 0.47162208 -0.53410155 0.4172037 0.5331871 0.09620747 0.10050209 0.75702655 -0.047052395 -0.94938934 -0.023197398 -0.519412 -0.12093674 0.13885036 -0.3116792 0.58785826 0.72878027 -0.16533051 0.29647776 0.0759554 0.72283596 -0.35069874 -0.15673232 0.5490732 -0.73514163 0.3479626 0.10882157 -0.25876132 0.48779795 -1.0811975 -0.21038097 -0.01318409 -0.35579512 0.8165927 -0.8240671 0.36605218 0.1216507 -0.22299036 -0.09330895 -0.79163766 0.35477725 -0.35548565 0.39042887 0.12415982 0.2042703 0.831929 -0.30851483 0.31233546 0.88820964 0.12270731 -0.13568652 0.03878006 1.0798723 0.056385178 0.48592398 0.24118 -0.895875 -0.6078344 -0.14668036 0.26164612 0.40309137 0.3893642 -0.5503412 -0.1018895 -0.3666536 1.3150369 -0.07203185 0.087906584 0.7595982 -0.26366323 0.8435318 -0.9420275 0.31510833 -1.315068 -0.412399 -0.47897327 -0.31686738 0.07943091 0.63984805 0.2415226 1.0891511 0.13428752 0.32805058 0.22152005 0.5012459 -0.2838702 0.019508425 -0.89559376 -0.4110269 -1.2855697 0.3078793 -0.5513207 0.20186408 -0.6931642 -0.3667551 0.86694217 0.17558587 -0.927482 -0.17592572 -0.32589924 1.0049601 0.6941614 1.2263421 -0.22953944 -0.15503527 -0.6158976 -0.17624578 0.27536672 -0.33485723 0.22395268 0.21177277 -0.008339778 -0.53319407 -0.9492347 -0.3231328 0.002876471 0.45275733 0.6326023 0.23103744 -0.8447424 0.052038588 0.083106995 -0.4965119 -0.24049434 -0.6501539 -0.6583528 -0.42559415 0.5046994 0.13465439 -0.049163688 -0.2679954 -0.08277833 0.28395408 -0.6548062 -0.01636838 0.42923677 -0.17045999 -0.49630532 0.235063 0.112993665 -0.20455424 0.036377292 0.09460148 -0.4477088 0.3620096 0.8126873 0.9158718 0.13335924 1.1990399 0.30597886 -0.020412255 0.16595681 0.0066588563 -0.23757082 -0.2184255 -0.0043512173 -0.03007321 0.0742151 0.6025173 0.38741404 -0.020744555 0.6948844 0.9036674 0.6146634 -0.47792393 -0.029537855 -0.41166735 0.5753102 0.26155382 -0.21807915 -0.23184082 -0.23517767 -0.6478374 -0.5534656 0.32736635 -0.07567799 0.43857834 -0.43502253 0.17669687 -0.7844124 -0.039588306
Original 1024 Dimensional Embeddings
-0.1265343 0.82008207 -0.110318914 -0.6100255 -0.5296021 0.015677562 0.11397815 0.53097856 -0.17499244 0.64392024 0.35149568 0.29564062 -0.02466401 0.065258086 -0.4745373 0.3802824 -0.26294824 0.54623055 0.5102224 0.22611201 0.30248043 0.20380855 -0.84067285 -0.31903073 -0.07415995 0.42553836 0.32857093 -0.0469367 0.7168652 0.16165186 -0.5318038 -0.63474494 0.20950772 -0.9052298 -0.088074334 -0.36755788 0.50429726 0.034378607 -0.9997739 -1.4656237 -0.010628737 0.3463953 0.5884347 0.2849783 -0.8844611 -0.206935 -0.71667355 -1.0084801 0.7276159 -0.5753827 0.07795743 0.76599026 0.1511684 0.78912795 0.0658147 -0.03566352 0.21439466 -0.6960161 0.430086 0.69442135 0.27248186 -0.22236401 0.31023797 -0.35163894 0.101938814 0.7694024 -0.24116729 0.21857552 0.18383402 -0.0565552 0.13785216 -0.1628346 -0.70273244 -0.47599787 -0.46279162 -0.19974774 0.47162208 -0.53410155 0.4172037 0.5331871 0.09620747 0.10050209 0.75702655 -0.047052395 -0.94938934 -0.023197398 -0.519412 -0.12093674 0.13885036 -0.3116792 0.58785826 0.72878027 -0.16533051 0.29647776 0.0759554 0.72283596 -0.35069874 -0.15673232 0.5490732 -0.73514163 0.3479626 0.10882157 -0.25876132 0.48779795 -1.0811975 -0.21038097 -0.01318409 -0.35579512 0.8165927 -0.8240671 0.36605218 0.1216507 -0.22299036 -0.09330895 -0.79163766 0.35477725 -0.35548565 0.39042887 0.12415982 0.2042703 0.831929 -0.30851483 0.31233546 0.88820964 0.12270731 -0.13568652 0.03878006 1.0798723 0.056385178 0.48592398 0.24118 -0.895875 -0.6078344 -0.14668036 0.26164612 0.40309137 0.3893642 -0.5503412 -0.1018895 -0.3666536 1.3150369 -0.07203185 0.087906584 0.7595982 -0.26366323 0.8435318 -0.9420275 0.31510833 -1.315068 -0.412399 -0.47897327 -0.31686738 0.07943091 0.63984805 0.2415226 1.0891511 0.13428752 0.32805058 0.22152005 0.5012459 -0.2838702 0.019508425 -0.89559376 -0.4110269 -1.2855697 0.3078793 -0.5513207 0.20186408 -0.6931642 -0.3667551 0.86694217 0.17558587 -0.927482 -0.17592572 -0.32589924 1.0049601 0.6941614 1.2263421 -0.22953944 -0.15503527 -0.6158976 -0.17624578 0.27536672 -0.33485723 0.22395268 0.21177277 -0.008339778 -0.53319407 -0.9492347 -0.3231328 0.002876471 0.45275733 0.6326023 0.23103744 -0.8447424 0.052038588 0.083106995 -0.4965119 -0.24049434 -0.6501539 -0.6583528 -0.42559415 0.5046994 0.13465439 -0.049163688 -0.2679954 -0.08277833 0.28395408 -0.6548062 -0.01636838 0.42923677 -0.17045999 -0.49630532 0.235063 0.112993665 -0.20455424 0.036377292 0.09460148 -0.4477088 0.3620096 0.8126873 0.9158718 0.13335924 1.1990399 0.30597886 -0.020412255 0.16595681 0.0066588563 -0.23757082 -0.2184255 -0.0043512173 -0.03007321 0.0742151 0.6025173 0.38741404 -0.020744555 0.6948844 0.9036674 0.6146634 -0.47792393 -0.029537855 -0.41166735 0.5753102 0.26155382 -0.21807915 -0.23184082 -0.23517767 -0.6478374 -0.5534656 0.32736635 -0.07567799 0.43857834 -0.43502253 0.17669687 -0.7844124 -0.039588306 -0.48291507 0.37091422 -0.33908314 0.2132256 0.08879693 -0.19823262 -0.11425367 0.2234637 0.20309447 0.002771456 -0.260877 0.7475132 0.045691293 -0.3815335 -0.37763008 -0.1969011 -0.1088352 0.019161811 -0.6240594 -0.07173541 1.5279161 0.1329002 0.20655955 -0.40820175 -0.18019912 -0.5849627 -0.39974803 0.63006645 0.26758248 0.59174037 -0.29012516 -0.40241337 -0.1365891 0.45351666 -0.47127104 0.2188159 -1.1867115 -0.8080662 0.43460304 -0.38791388 -0.7232234 0.014113191 -0.10334038 -1.1203644 -0.3001314 -0.6143357 -0.3500347 -0.72640127 0.04617742 1.092367 -0.50006115 -0.26411718 0.37396905 0.018781876 0.0806275 0.68014306 -0.108136274 -0.019995982 -0.43456346 0.032233693 0.66279894 -0.08621318 -0.65623045 -1.2803018 0.06505166 0.1675148 0.18619302 -0.15584388 -0.029591527 0.5783873 0.47783896 -0.6557989 0.52203304 -0.33270928 -0.53737146 -0.92110455 -0.33646533 0.7206859 -1.0200963 -0.58409196 -0.13549729 -0.16298807 -0.24182247 0.04137627 1.4189351 -0.9435172 -0.033530526 -0.15904075 -0.21153675 0.48610753 0.6449688 -0.62298113 0.26005617 -0.07057297 -0.31858474 -0.28219575 0.3068475 0.20287614 -0.12749258 0.13714638 0.028180066 0.982986 -0.6955943 -0.0025826886 0.23391466 0.12779367 -0.4374205 -0.3236497 0.022197248 0.32421684 -0.62082547 0.34360278 0.29678556 -1.0925034 -0.3412331 0.38284442 -0.9668197 -0.33886617 0.4538325 -0.6718355 0.6702118 0.1229792 0.17488387 0.015265303 0.19751483 -0.24965094 0.58180124 0.748483 0.6634381 0.03220409 0.14171897 0.20350817 -0.1799155 0.2688538 0.24591918 0.18081564 0.48646826 0.07041702 -0.868582 -0.611362 0.7380996 0.35994574 0.78340816 -0.09039226 0.33257544 1.0214131 0.56971765 -0.3046297 -0.93025213 -0.5596697 -0.05586979 0.5848395 0.3126951 -0.08618602 0.32091343 -0.42081285 -0.20357889 0.05943345 -0.62088394 -0.026739784 -0.60921955 0.11146992 -0.3973027 -0.18798876 -0.5722979 -0.0020868185 -1.2055811 0.8563994 0.6399509 -0.5981984 0.3637058 -0.78832114 0.37062746 0.26096538 0.25578654 -0.37302828 0.19956078 0.49382967 -0.5952309 -0.07803636 -0.4164723 0.8528953 0.42942092 -0.14286116 0.64120036 0.56303406 -0.24771057 -0.5545252 -0.14938562 -0.72367764 0.0033274312 0.22349262 -0.24992737 0.056585543 0.52416784 -0.117646046 -0.1914711 -0.2347065 0.15017594 -0.60897934 0.62384796 0.6927745 0.8098773 -0.14852048 0.17611481 -0.3707282 0.6116622 -0.4622789 -0.38333595 0.49030194 1.2002004 -0.58979183 0.5439781 0.2092785 -0.9323804 0.39692843 -0.3384574 0.09816061 0.023693109 -1.0219014 0.28319407 0.11798043 -0.14411774 0.7834707 -0.38426304 0.25736576 0.47558847 -0.19797978 -0.3171102 -0.37177 0.2608961 0.8457771 -0.60360265 0.8077115 -0.6006631 0.12261704 0.16604069 -0.46812636 -0.0073651643 0.18431656 -0.92258376 0.31228125 -0.0073801572 -0.5085064 -0.13612896 -1.2111968 -0.07150262 0.1629142 -0.48276028 -0.4458793 -0.8898111 1.025041 -0.19731075 0.89314103 -0.10910203 0.9432207 0.4755921 0.036895186 -0.78342384 0.19327122 0.62933356 0.053962223 0.15122883 1.0833378 0.25922316 -0.5659045 0.062609255 0.045444157 -0.046508167 0.061830293 0.11505561 0.43599924 -0.13634953 -0.9643307 0.12282005 -0.85537857 -0.26923993 -0.67377204 -0.27149048 -0.004454697 0.06176404 -0.35835788 -0.29283926 1.0668949 -0.03523527 -0.39540705 0.1722646 -0.29390705 0.045052446 0.31655297 0.34101066 -0.21340111 -0.24971369 -0.75681955 0.25547296 1.0705259 -0.30574164 -0.4461546 -0.51718044 -0.7591734 0.1842232 0.24742308 0.33655304 0.093732394 -0.6944431 0.5055424 -0.32505628 -0.12044382 -0.56428975 -0.49904722 -0.15654801 0.5816177 1.201608 0.11852671 -0.082083076 0.16668011 1.3404951 -0.12145783 0.10639885 -0.55174816 -0.93952394 -0.53135985 -0.2358879 0.27863124 0.022789165 0.059557695 -0.4756727 -0.9178567 0.22335127 -0.2373191 -0.2837195 0.014570179 -0.30928284 0.5060707 -0.68515384 0.53970873 0.402473 -0.22675714 -0.6647435 0.23192304 -0.5349888 0.38113672 -0.25379056 -0.22788498 -0.7996721 -0.60675937 -0.25999704 -0.62695396 -0.08003291 -0.6542564 -0.1253941 0.16758697 0.6106187 -0.24024965 -0.4967656 0.49760357 -0.36426646 -0.41620603 0.21890171 0.6291589 0.9447894 -0.26228878 0.8192878 0.060836073 -0.24502455 0.5184602 0.741826 0.2676298 -0.112392515 -0.57440174 0.86978054 -0.2833799 0.80018485 0.2214977 0.45686817 -0.2221589 0.326996 0.1151191 0.82493585 -0.11747769 -0.23925772 0.019947397 -0.98603487 -0.51873326 0.38105232 0.28463495 -0.011481924 -0.11758184 -0.28690577 -0.5577888 0.5784941 -0.42450935 -0.40468925 -0.24989654 0.15958954 -0.0847187 0.79291683 -0.28794146 0.0017874032 -0.09327816 0.1010029 -0.5699648 0.80102384 -0.14354149 -1.0119303 0.10845255 -0.12285681 -0.6320803 0.23861603 0.69925165 0.6542826 -0.20199767 0.37254056 0.2903379 -0.17243016 -0.48065785 -0.6669654 0.39595708 0.65378296 0.26887307 -0.38379928 -0.06944079 0.168138 0.29253173 -0.3608925 0.031845592 0.060253303 0.09446708 0.24829516 -0.122476146 0.12554221 -0.34127146 -0.12290917 0.48619106 -0.18212983 0.043750226 0.87400407 0.33520538 -0.13858712 0.26271534 -0.2983128 -0.4876674 0.15607636 -0.9369842 -0.20255376 -0.13822876 0.4087381 0.67684686 0.2527273 0.16865413 0.7026079 -0.028893115 -0.5917334 -0.37510088 -0.6393557 -0.5105761 0.72096014 -0.7052822 -0.65928173 -0.10481483 -0.5710433 0.20483916 0.04889236 -0.52506196 0.9455462 -0.22449477 -0.5362858 -0.6421528 0.70837605 1.204418 -0.32374567 -0.17750661 0.5112475 -0.037233256 0.46613193 0.41136405 0.3181547 -0.19938204 0.23804134 -0.3504183 -0.667518 -1.1102188 -0.49256438 -0.08048176 0.8166891 -0.7815312 -0.20702662 0.5644025 -0.17680104 -0.1131974 0.4685566 -0.034961212 -1.062612 0.520129 -0.6423693 0.3618085 0.10217163 -0.5374255 -0.36155972 -0.45183298 -0.15997744 -0.8096759 0.3007736 0.7844794 0.40965706 -0.78665936 -0.53652066 0.42966467 0.32520396 0.60054284 -0.66331774 -0.14583653 0.81720793 0.35755882 -0.31127182 0.39301708 0.14712577 -0.31566173 0.096749574 0.5010104 0.7469416 -0.75171536 0.42801854 -0.5516398 0.24478175 0.28076455 0.04525625 0.3824216 -0.18659772 -0.53181034 -0.54974866 0.115223385 0.28835753 -0.20140412 0.14141183 0.25533915 0.56368595 -0.25716466 -0.85495234 0.62309337 0.40922248 -0.2793142 -1.0161443 0.50703 0.57825655 -0.22924392 -0.31337622 0.95607734 -0.0960989 -1.6038705 0.022548188 -0.096831985 0.20567599 -0.2645024 -0.41407788 0.18379086 -0.4675033 -0.42981836 0.10494639 -0.4994938 0.6598088 -0.77465063 -0.4816524 -0.5510564 0.09036474 -0.5320895 0.1411781 0.29003668 0.54947406 0.02463306 0.39512673 -0.06474627 0.5100985 0.50939643 0.1225233 -0.5879439 0.39677677 -0.49017274 0.05685936 1.0140077 0.3752742 0.5886367 0.09883715 0.33191127 0.26961824 0.7071267 -0.88264567 -0.32347602 -0.27539983 -0.7062862 -1.6820498 -0.13621008 0.55857205 -0.8185455 0.27574474 0.57132053 0.0028187656 -0.07343531 0.07138754 0.36514786 -0.1466676 0.46095297 0.19000141 -0.30571347 0.090632185 -0.2282337 0.34922102 -0.6024745 -0.78775704 -0.52378386 -0.60978425 -0.44716373 -0.024772579 -0.34074235 0.05717966 -0.44404885 -0.959487 0.24570718 -0.39314023 -0.19661818 0.20936638 0.40629125 1.26162 -0.42331925 -0.36336204 0.1518829 -0.30125114 0.48335248 -0.35274464 -0.22297281 0.2512738 0.52284676 -0.66088605 -0.54570913 0.0068584955 -0.3713614 -0.3694186 -0.6969237 0.4111469 0.9105379 -0.13406044 0.024038501 -0.29087925 -0.37907106 0.91156 1.4272813 -0.31485906 0.5307218 0.3171659 1.0181988 0.5415143 0.5915739 0.20318039 -0.90045476 0.13267668 -0.791834 -0.019502757 -0.12623908 -0.08142469 -0.028820753 0.3477391 -0.26536736 -0.72524256 0.47415206 -0.9138102 -0.48330313 -0.2073152 -0.11168104 0.088617064 0.00068150973 0.62993735 0.45730442 0.13548496 4.2387786 0.6750245 0.5104254 0.75578195 0.15242855 0.43684548 0.02986786 -0.115987174 0.26951838 -0.40221444 -0.69370055 -0.39567867 0.5606212 0.34129506 0.1679893 0.7285181 -0.2414775 0.52145576 0.27154323 -0.232309 -0.6774989 -0.230428 -0.23153955 0.19381408 0.11591116 0.41071877 0.2821337 0.021200325 -0.7813165 -0.34544313 0.4543501 -0.36588368 0.1074448 -0.5368601 -0.3512965 0.847254 0.047630787 -0.39580244 0.245927 -0.14029205 0.28046566 -0.24657203 0.13135749 -0.7204971 0.38578746 0.21177253 -0.38903365 -0.7786522 1.0735209 -0.31094965 0.8617428 -0.2780682 0.8150008 0.6725559 0.13614391 0.7553265 0.6900425 -0.28700814 0.26259097 0.06866645 0.9755453 -0.24464822 -0.53193605 -0.40035516 -0.022782134 0.53123325 0.8269285 0.6653648 -0.19781779 -0.014016478 0.069808625 0.3219856 -1.2654588 -0.2028693 0.6068143 0.3148606 0.11555031 0.070121 -0.34351382 -0.67531425 0.574347 -0.341136 -0.36103526 0.40552172 -0.124884024 -0.09707443 -0.3533114 0.0015976208 -0.39007822 0.1735838 0.7387476 0.52283067 -0.4928086 -0.8002257 0.35249114

Leave a Reply